When I first learned about Cascade Models I become interested in how does the topology of a graph influences the dynamics of cascades on that graph. Is it possible to test graph isomorphism by comparing some statistics of cascade models on different graphs? I summarized some of my ideas in the preprint, but didn’t really tried to publish it, since the isomorphism test looks too complicated, and, I suppose, that it is not significantly faster than traditional methods. My hope was that it can provide better non-isomorphism certificates, but this topic requires more thorough investigation.

However, I found out that a Game of Life on Graphs, that I suggested in the preprint, exhibits an interesting behaviour and is worth to discuss in this blog post.

Game of Life

Conway’s Game of Life is a foundational example of cellular automata. Its main purpose was to show, how easy is to construct a Turing-complete system of rules. People have found various live patterns, static and moving, see example from the library. A Game of Life implementation of Turing Machine may be found here.

Game of Life on Graphs

Game of Life on Graphs is a discrete-time dynamical system on a graph $G = (V, E)$, similar to a system defined in my previous blog post. At every time step, every vertex $v\in V$ is in one of two possible states ‘Alive’ or ‘Dead’. Initially, at time $t=0$, some vertices $v\in A_0 \subseteq V$ are alive and all other vertices $v\in D_0 = V\setminus A_0$ are dead. The major difference is that Game of Life on Graphs evolves deterministically; no probability is involved and the system dynamics is completely determined by $A_0$ and integer parameters $\mathfrak a$, $\mathfrak d$ and $\mathfrak r$. Then, the system evolves following the rules below:

• Any alive vertex with fewer than $\mathfrak a$ alive neighbors dies, as if by underpopulation.
• Any alive vertex with less than $\mathfrak d$ dead neighbors dies, as if by overpopulation.
• Any dead vertex with exactly $\mathfrak r$ live neighbors becomes a live cell, as if by reproduction.

Examples

Some experiments are available on my github. Meanwhile, let’s consider a couple of simple illustrations. In this post, I mostly consider a Game of Life with parameters $\mathfrak a = 1$, $\mathfrak d = 1$ and $\mathfrak r = 1$, since according to my experiments it givens the most complex patterns for small graphs with up to 10 vertices. However, any other values of parameters are possible.

The first example is a complete graph on five vertices and one of them is initially alive. In this case, the initially alive vertex dies by underpopulation, but gives life to other four. Starting from the second step, Life becomes still:

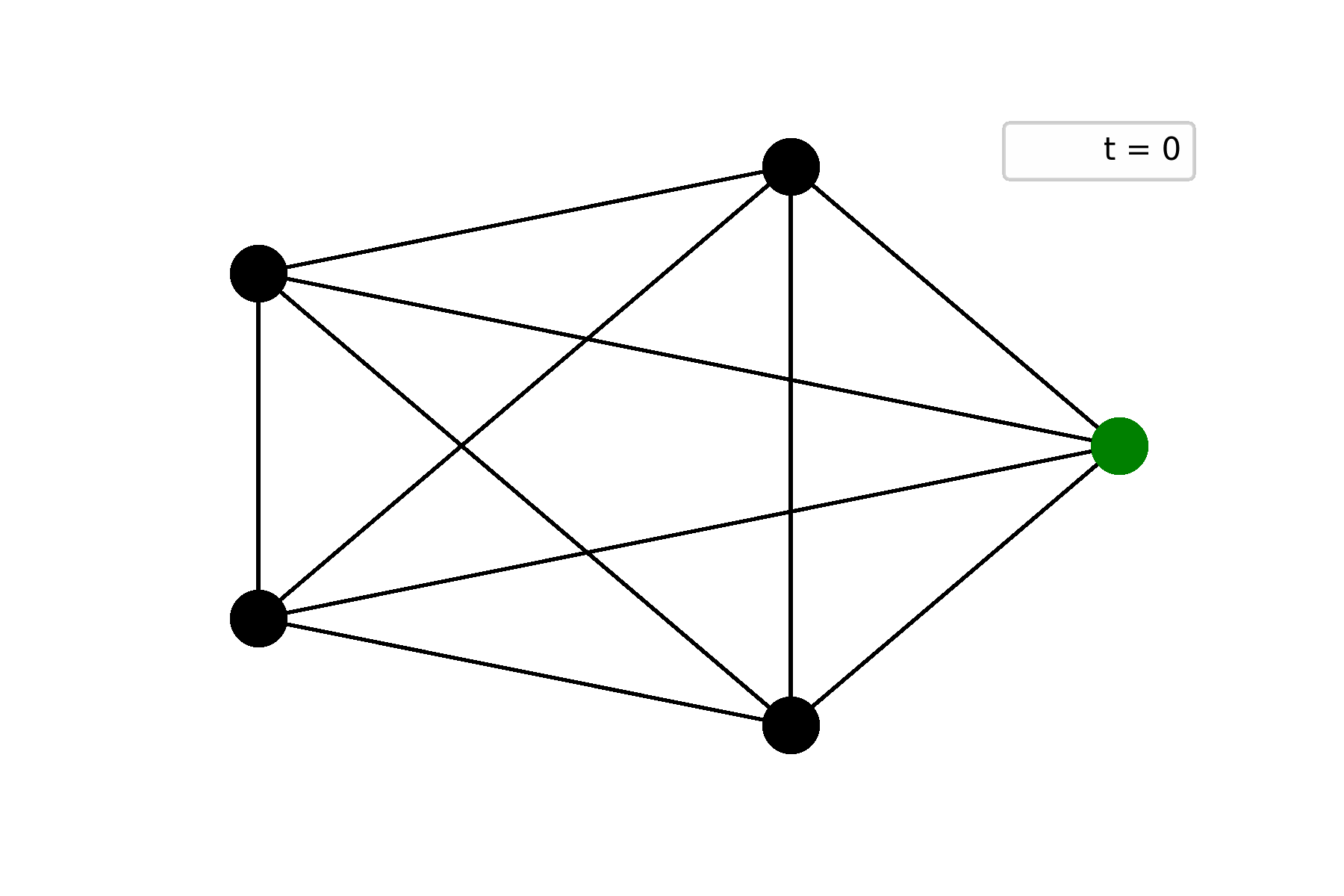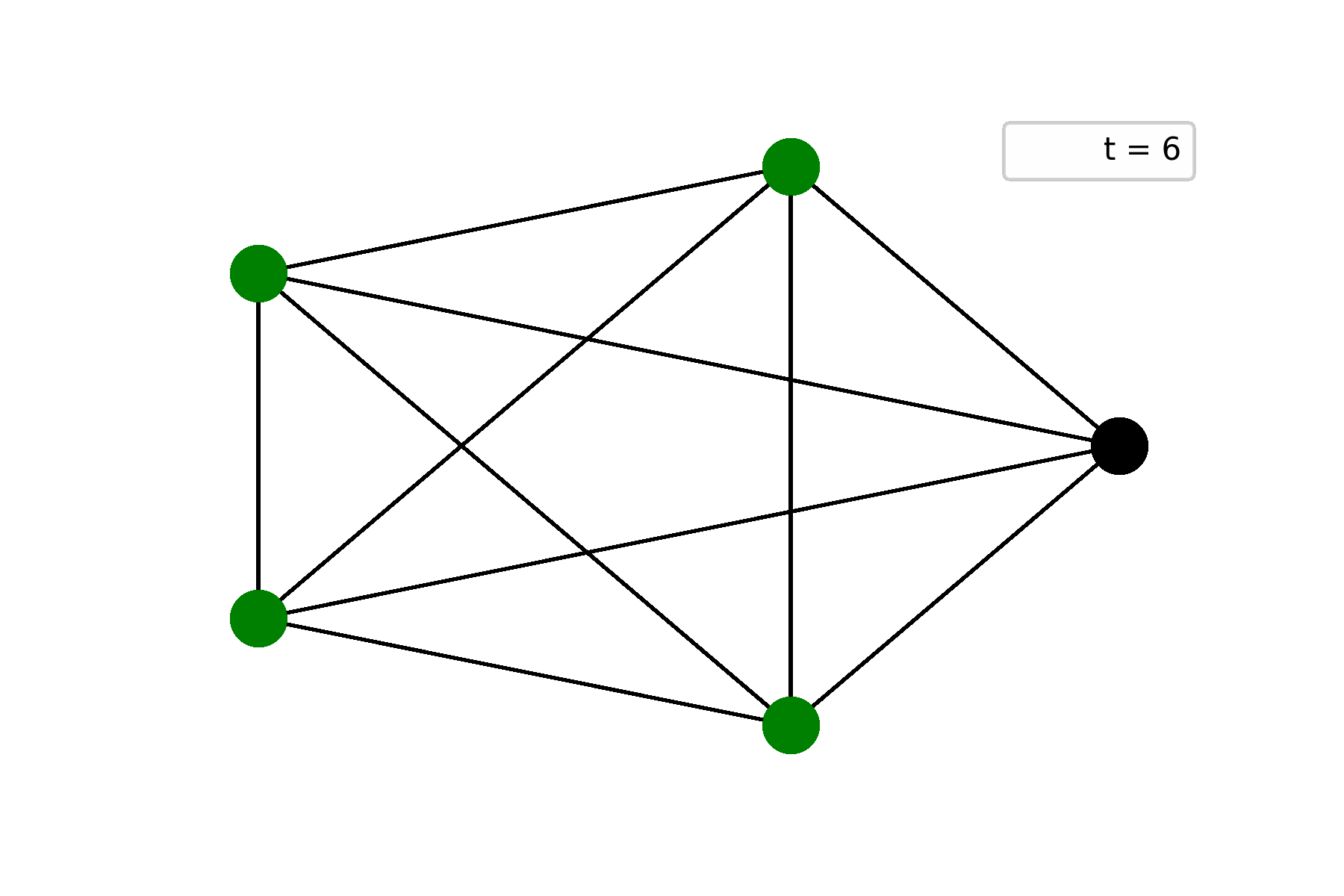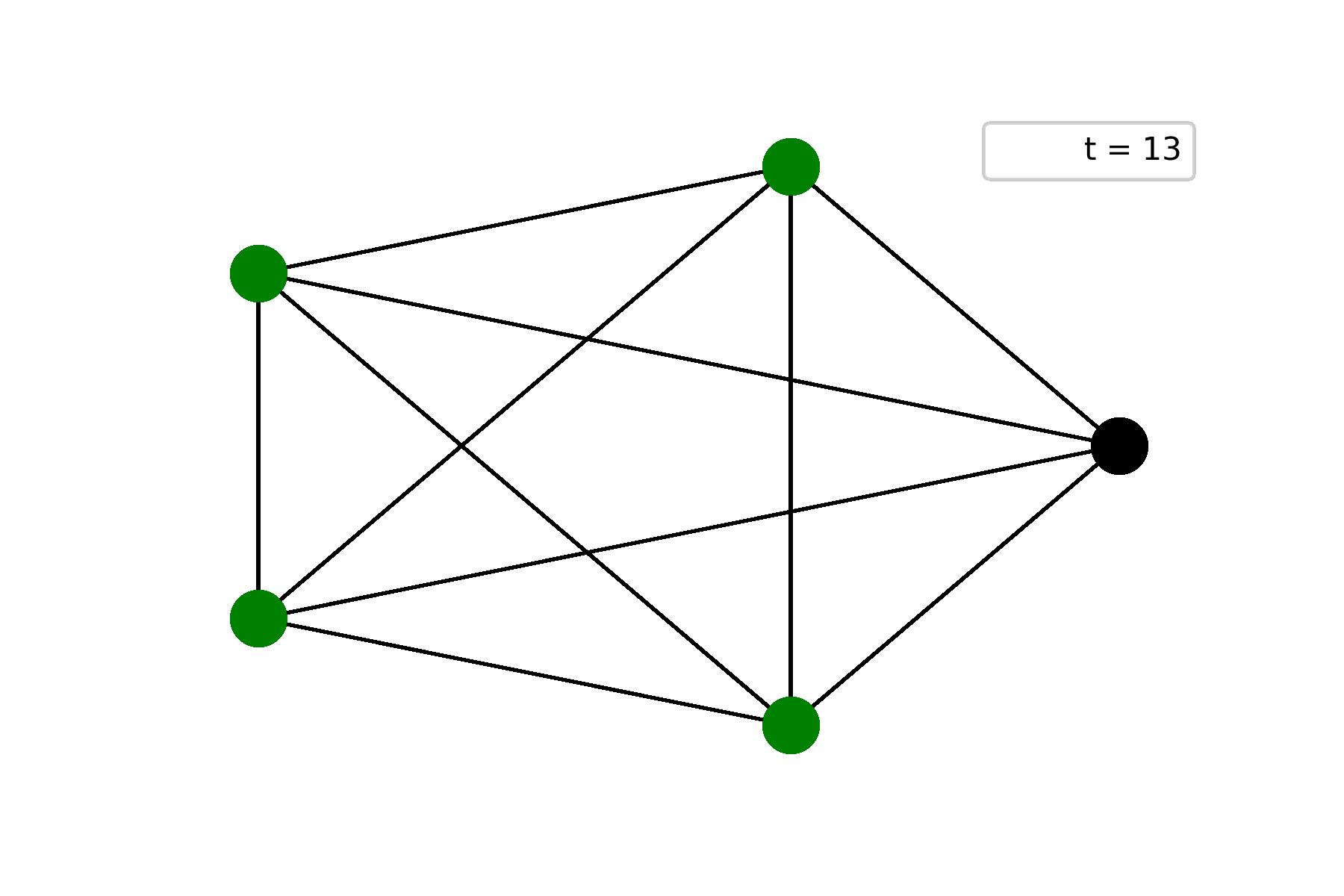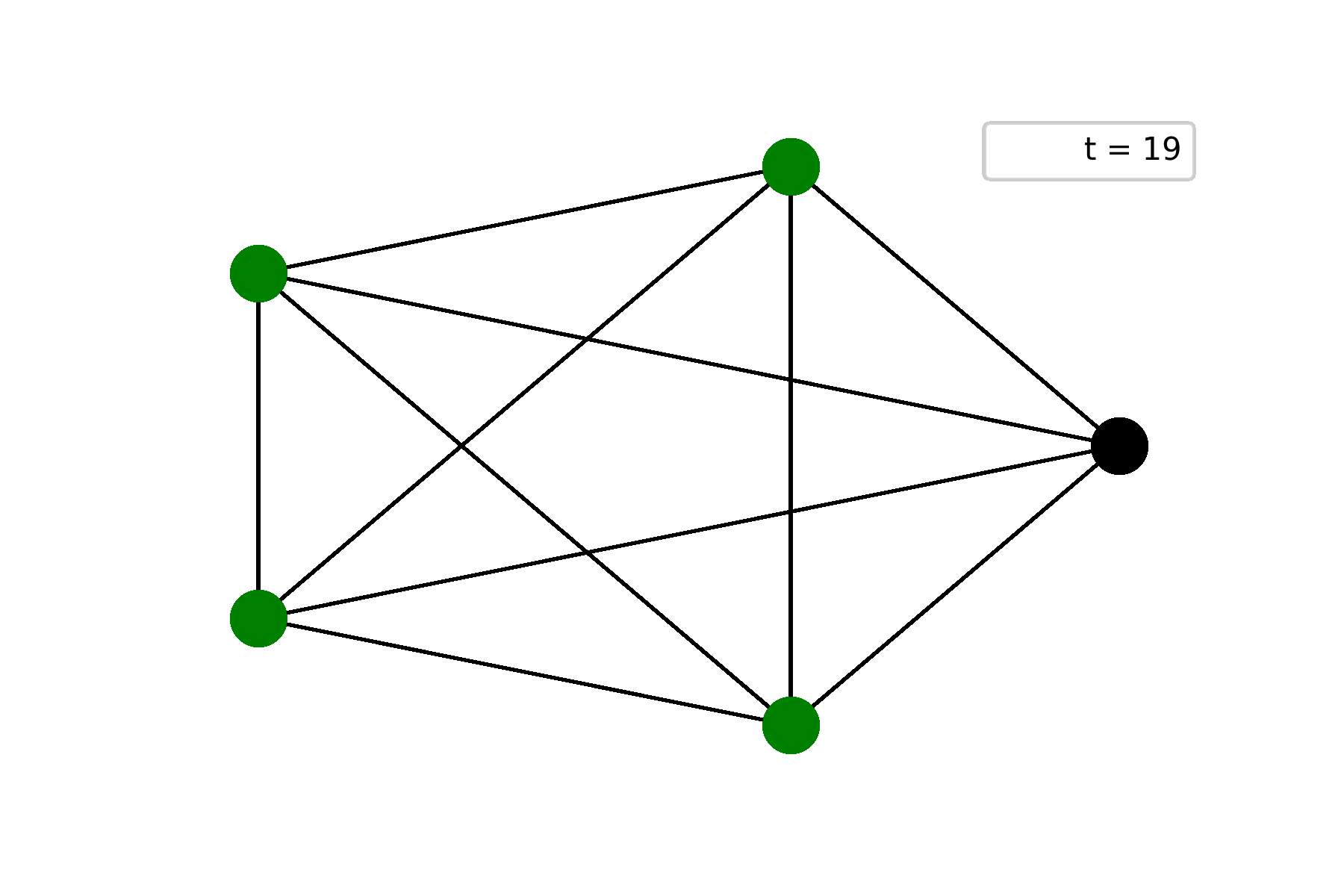
The second example is a path graph on five vertices and one of end-nodes is initially alive. In this case, Life repeats itself at step $t = 6$ and starts to oscillate:

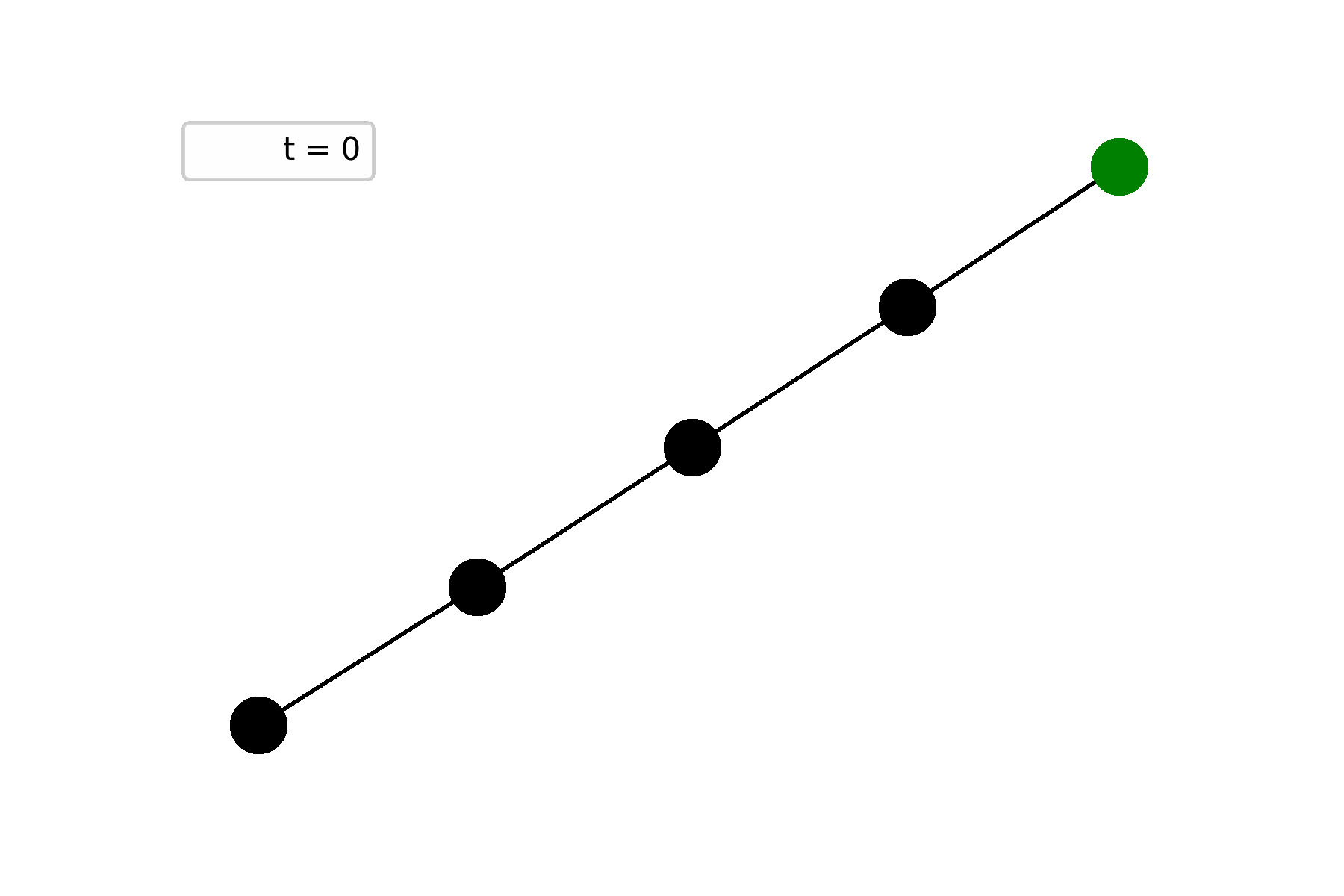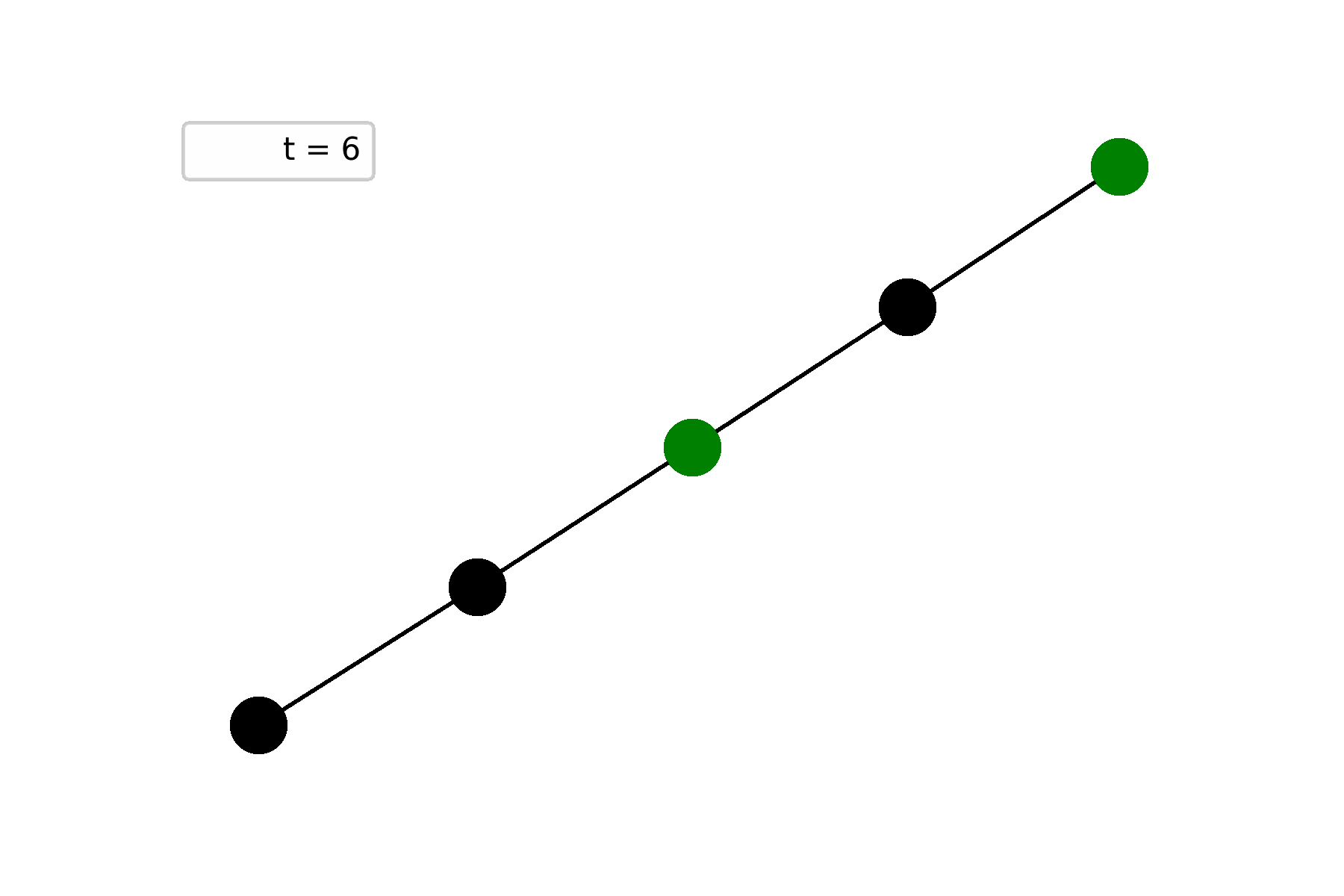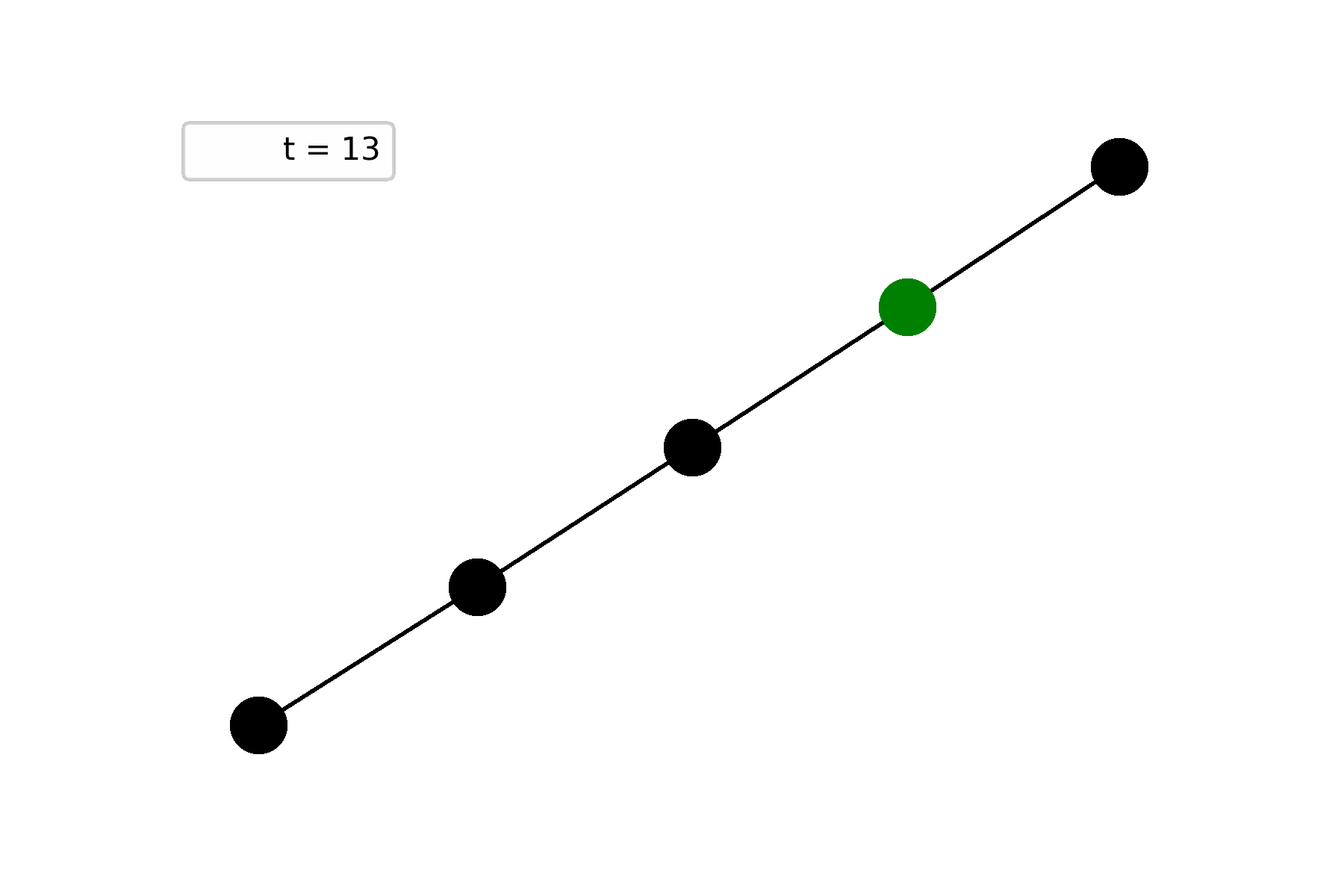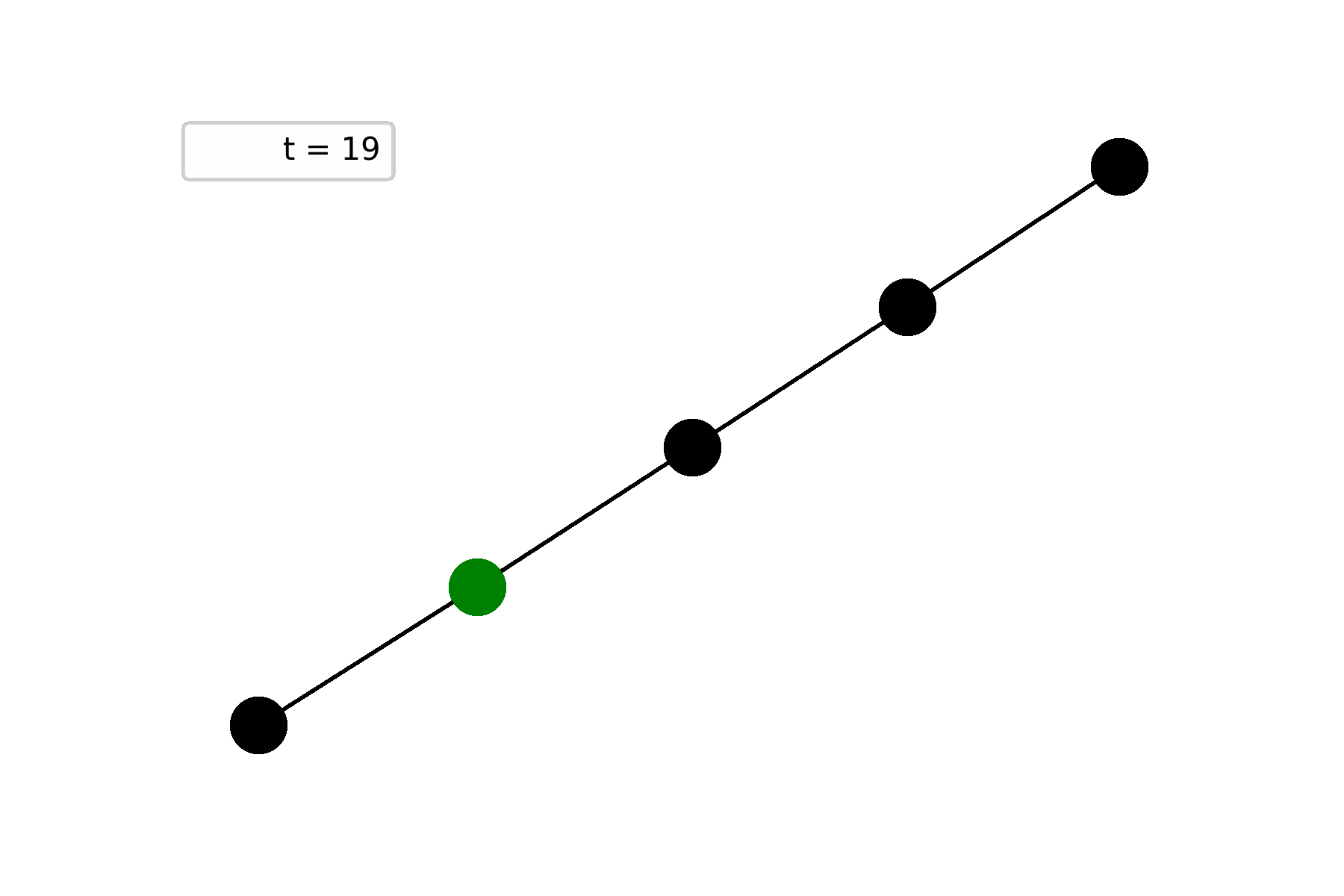
Universality

Note that Conway’s Game of Life is an instance of the Game of Life on Graphs. Let us consider an infinite grid graph: 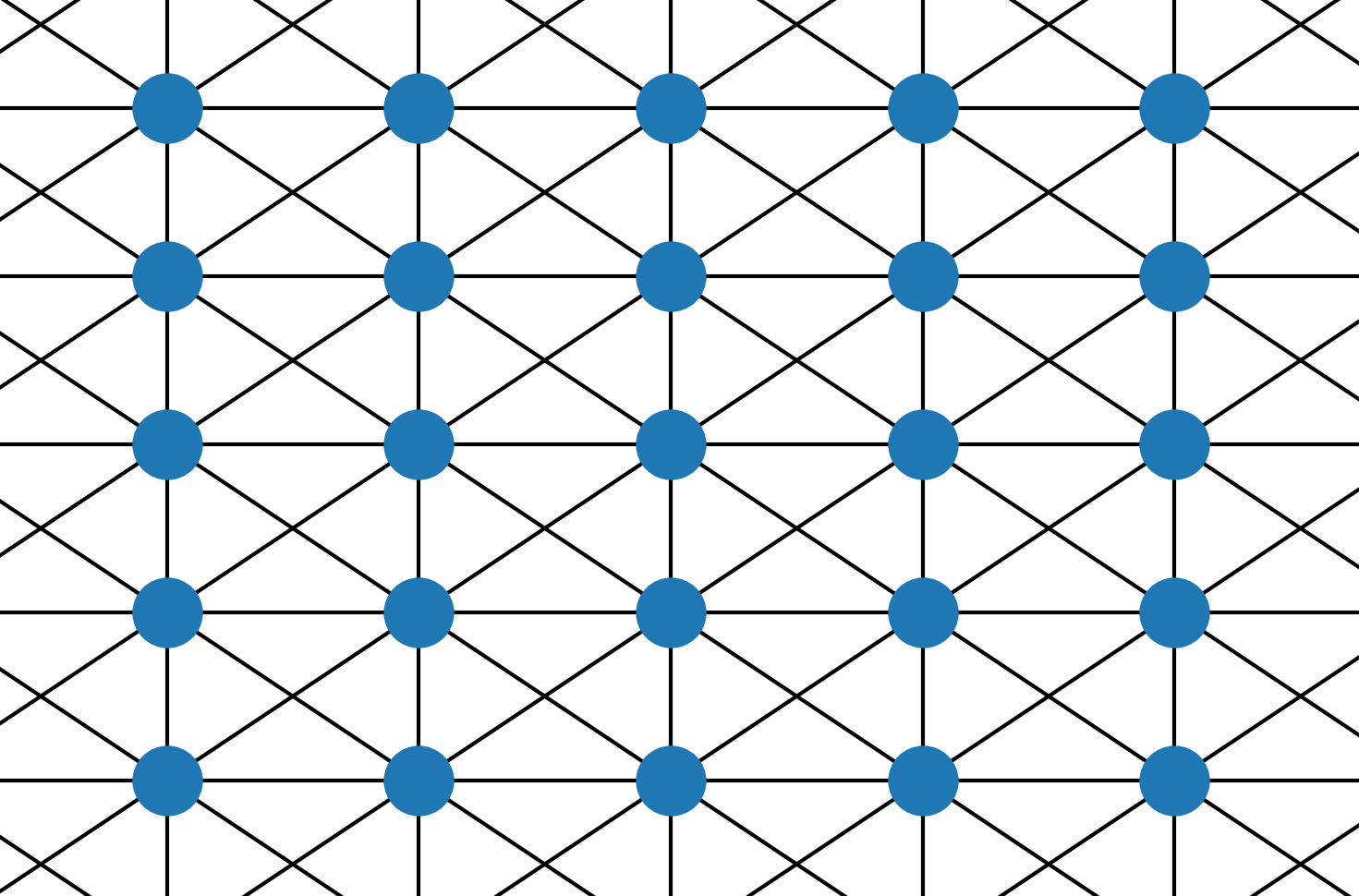a set of initially alive vertices $A_0$ and an instance of Game of Life on Graphs with parameters $\mathfrak a = 2$, $\mathfrak d = 5$ and $\mathfrak r = 3$. This instance of the Game of Life on Graphs is equivalent to Conway’s Game of Life and thus Game of Life of Graphs is also Turing Complete (if we allow infinitely large graphs).

To be continued…