I first learned about Gabriel Graphs when our team faced the problem of random planar network topology generation. There are many other beautiful models known such as Urquhart and Relative neighborhood graph. In this post, I will demonstrate a few ways to generate random Gabriel graphs in Pure Python.

Gabriel Graph Definition

Graph $G$ is called Euclidean, if its vertex set $V$ is embedded into a plane equipped with Euclidean distance. Gabriel graph is a Euclidean graph that satisfies the following criterion: any two vertices $p, q \in V$ are connected by an edge if and only if the circle with diameter $pq$ contains no other vertex from $V\setminus {p, q}$.

Gabriel graphs are closely related to Delaunay triangulations and Voronoi diagrams. Gabriel graphs are subgraphs of the corresponding Delaunay triangulation, and Voronoi diagrams can be used for graph generation as we will see below.

Some Examples

First, for our experiments we need the following imports:

import itertools
import networkx as nx
import numpy as np
from scipy.spatial import Delaunay
from scipy.spatial import Voronoi, voronoi_plot_2d
import matplotlib.pyplot as plt

Gabriel graph generation starts with sampling $n$ points on the euclidean plane. In the figure below we sample 20 points and build their Delaunay triangulation:

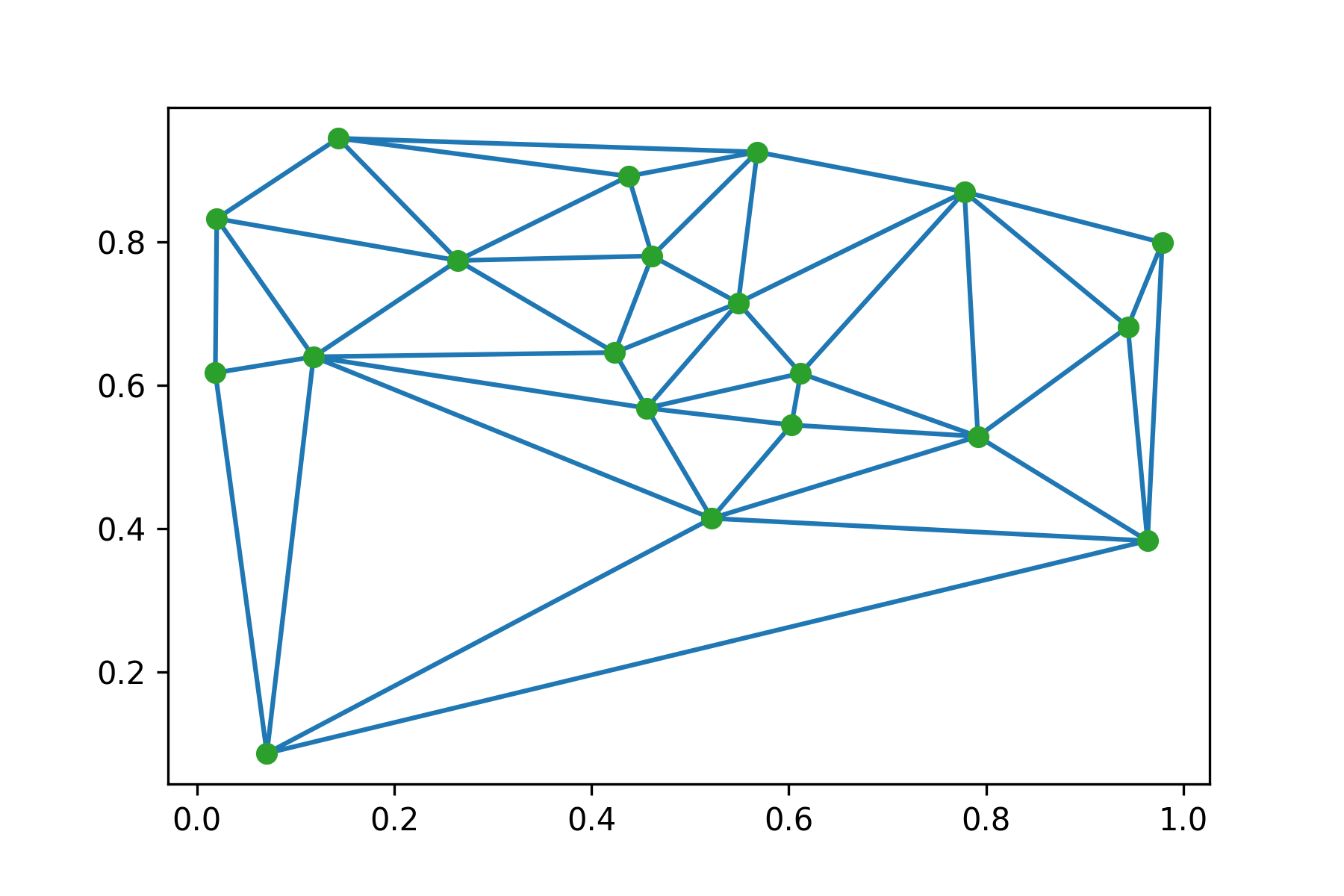
The Voronoi diagram of the same set of points is shown below, it will be used later for efficient Gabriel graph generation:

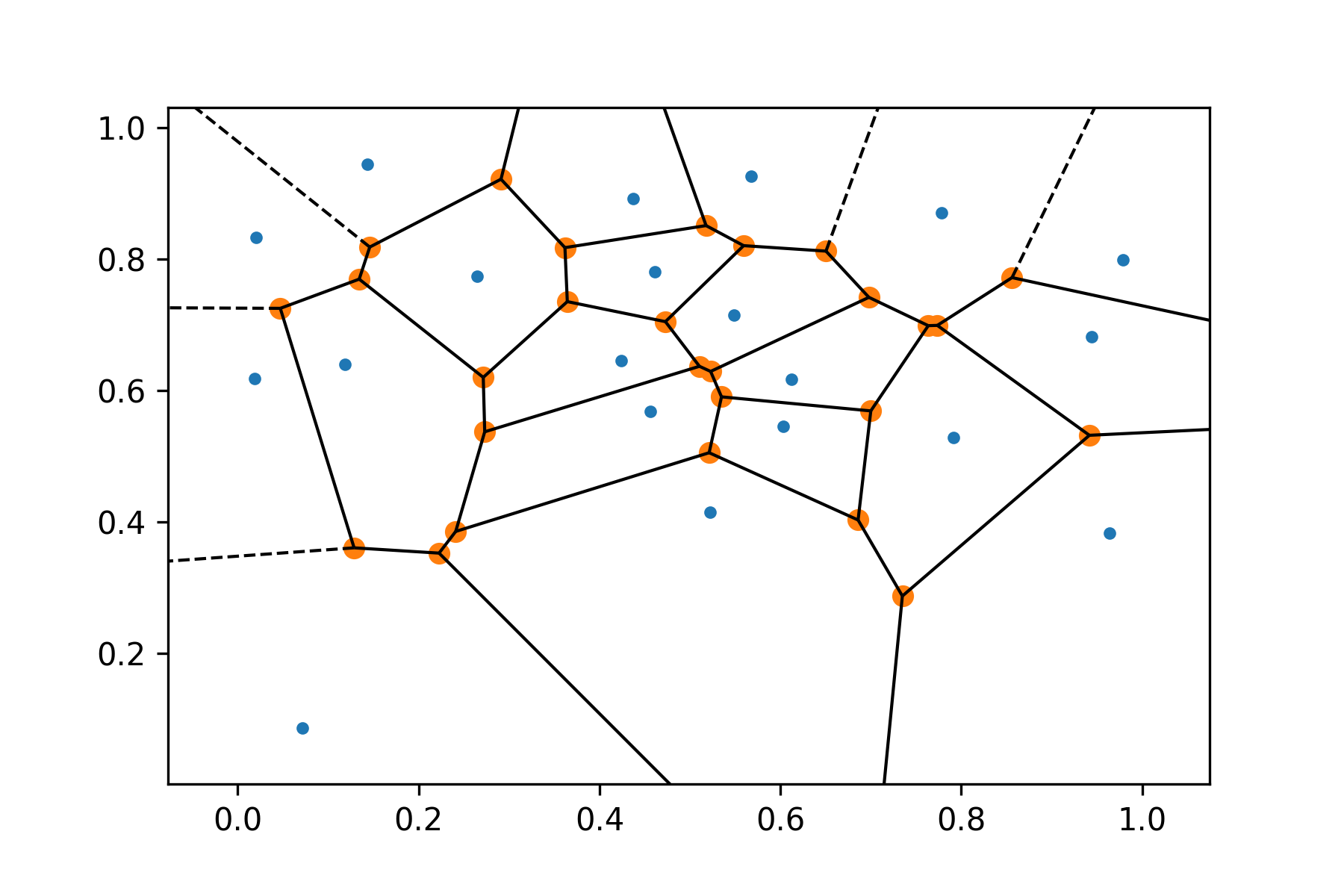
And finally (spoiler!) let’s plot the Gabriel graph of this set of points:

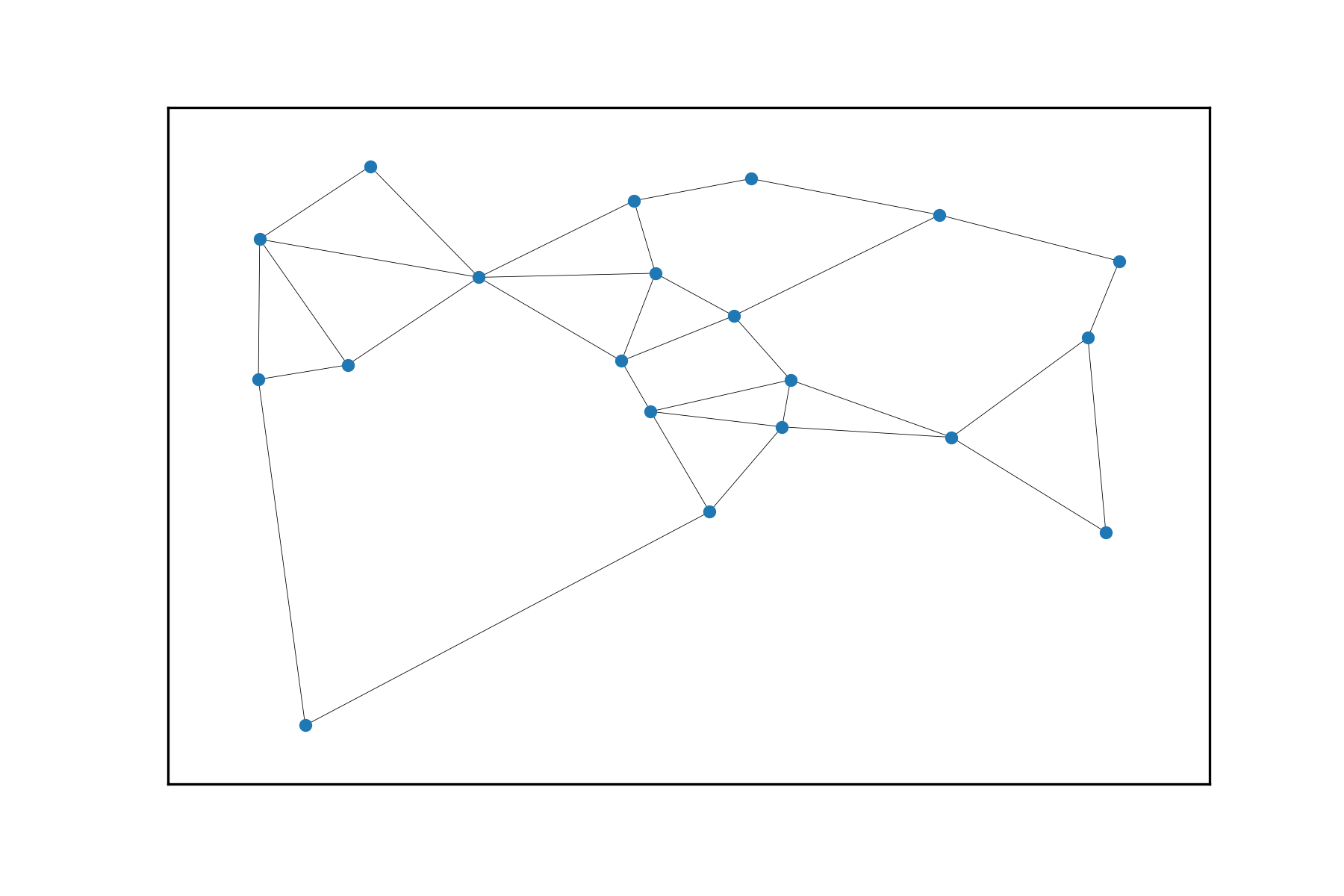
Algorithms: Bruteforce

The first and most straightforward method to build a Gabriel graph from a set of points does not even involve Delaunay triangulation. We can simply iterate all triples of points and check the criterion from the Gabriel graph definition. The method has cubic complexity and is ok for small graphs with up to a few hundreds of vertices:

def GabrielViaBruteforce(n, seed=None):
    G = nx.complete_graph(n)
    np.random.seed(seed)
    coordinates = np.random.uniform(0, 1, 2*n)
    points = coordinates.reshape(-1, 2)
    
    triples = itertools.product(range(n), repeat=3)
    for triple in triples:
        if (len(set(triple)) != 3) or (triple[0] not in G.neighbors(triple[1])): continue
        p1 = points[triple[0]]
        p2 = points[triple[1]]
        p3 = points[triple[2]]
        center = 0.5 * (p1 + p2)
        radius = 0.5 * np.linalg.norm(p2-p1)
        if (np.linalg.norm(p3-center) <= radius):
            G.remove_edge(triple[0], triple[1])
            
    return G, points

Algorithms: Delaunay

A more clever way to construct a Gabriel graph relies on the fact that Gabriel graphs are subgraphs of the corresponding Delaunay triangulation. Thus we can find Delaunay triangulation in $O(n \log{n})$:

def DelaunayGraph(points):
    tri = Delaunay(points)
    G = nx.Graph()
    
    indptr = tri.vertex_neighbor_vertices[0]
    indices = tri.vertex_neighbor_vertices[1]
    for i in range(len(points)):
        for j in indices[indptr[i]:indptr[i+1]]:
            if i < j:
                G.add_edge(i, j)
                
    return G

Now for every edge of triangulation iterate all other nodes and check the condition. This gives an algorithm with $O(n\log{n} + mn)$ complexity where $m$ is the number of edges in triangulation:

def GabrielViaDelaunay(n, seed=None):
    np.random.seed(seed)
    coordinates = np.random.uniform(0, 1, 2*n)
    points = coordinates.reshape(-1, 2)
    gabrielGraph = DelaunayGraph(points)
    
    for e in gabrielGraph.edges():
        for other in gabrielGraph.nodes():
            if other not in e:
                p1 = points[e[0]]
                p2 = points[e[1]]
                p3 = points[other]
                center = 0.5 * (p1 + p2)
                radius = 0.5 * np.linalg.norm(p2-p1)
                if (np.linalg.norm(p3-center) <= radius):
                    gabrielGraph.remove_edge(e[0], e[1])
                    break
    
    return gabrielGraph, points

Algorithms: Delaunay and Voronoi

An even more fast algorithm after generating the Delaunay graph does not iterate all other points but uses a Voronoi diagram to check the condition. Here we use the easy fact that an edge $e$ of Delaunay triangulation is in the Gabriel graph iff $e$ intersects the boundary of the two corresponding Voronoi regions. Below we provide a fast Python implementation of segment intersection from here:

def ccw(A,B,C):
    return (C[1]-A[1]) * (B[0]-A[0]) > (B[1]-A[1]) * (C[0]-A[0])
def intersect(A,B,C,D):
    return ccw(A,C,D) != ccw(B,C,D) and ccw(A,B,C) != ccw(A,B,D)

The fast algorithm works as follows. We iterate the edges of triangulation and find two corresponding regions of the Voronoi diagram. If two regions share a border, there are two cases to consider: the border either contains the point at infinity or not. In the first case, we must first substitute the point at infinity with some large but finite point, so that the segment intersection works correctly.

def GabrielViaDelaunayVoronoi(n, seed=None):
    
    np.random.seed(seed)
    coordinates = np.random.uniform(0, 1, 2*n)
    points = coordinates.reshape(-1, 2)
    
    delaunayGraph = DelaunayGraph(points)
    voronoiDiagram = Voronoi(points)
    voronoiVertices = voronoiDiagram.vertices
    voronoiCenter = voronoiDiagram.points.mean(axis=0)
    ptp_bound = voronoiDiagram.points.ptp(axis=0)
    
    gabrielGraph = nx.Graph()
    for u, v in delaunayGraph.edges():
        uRegion = set(voronoiDiagram.regions[voronoiDiagram.point_region[u]])
        vRegion = set(voronoiDiagram.regions[voronoiDiagram.point_region[v]])
        boundary = sorted(list(uRegion.intersection(vRegion)))[-2:]
        boundaryVertices = [None, voronoiVertices[boundary[1]]]
        
        if (boundary[0] == -1):
            tangent = points[u] - points[v]
            tangent /= np.linalg.norm(tangent)
            normal = np.array([-tangent[1], tangent[0]])
            
            midPoint = 0.5 * (points[u] + points[v])
            direction = np.sign(np.dot(midPoint - voronoiCenter, normal)) * normal
            farPoint = voronoiVertices[boundary[1]] + direction * ptp_bound.max()
            boundaryVertices[0] = farPoint
        else:
            boundaryVertices[0] = voronoiVertices[boundary[0]]
        
        if intersect(points[u], points[v], boundaryVertices[0], boundaryVertices[1]): 
            gabrielGraph.add_edge(u, v)
    
    return gabrielGraph, points

Final: Some Animations

Using some code from the previous post I want to show how the topology of Gabriel graphs changes when we sample additional points on the plane:

def gabriel_gif(max_iter=20, seed=1):
    fig, ax = plt.subplots()
    
    def animate(i, shift, ax):
        ax.clear()
        ax.axis('off')
        gabrielGraph, points = GabrielViaDelaunayVoronoi(i+shift, seed=seed)
        nx.draw_networkx_nodes(gabrielGraph, points, node_size=2, ax=ax)
        nx.draw_networkx_edges(gabrielGraph, points, width=0.2, ax=ax)
        ax.plot([], [], ' ', label="n = {}".format(i+shift))
        ax.legend()
        
    life_animation = animation.FuncAnimation(fig, animate, 
                                             fargs=(4, ax),
                                             save_count=max_iter, 
                                             interval = 1000, 
                                             repeat = False)

    life_animation.save('gabriels.gif', writer='imagemagick', fps=0.66, dpi=300)